Comment coder une figure en géométrie

• «Lorsque l’on dessine une figure géométrique, on utilise des codes pour rendre la figure parlante  » dit le maître à l'élève.

• « Ouaouhhh ! » s'exclame ce dernier avant d'ajouter « Elle parle quelle langue ? »

• « Ooooh putain, c'est pas gagné » murmure le maître tout caressant amoureusement sa nuque. (La sienne... hein ! Pas celle de l'élève, bande de pervers !)

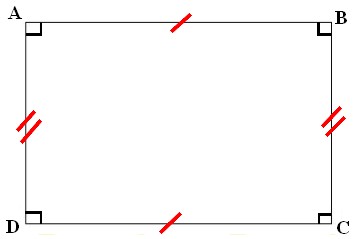
Pour indiquer que deux longueurs sont égales, on utilise des signes particuliers sur les segments qui sont de même longueur. Oulaaa... je vois que j'en ai déjà perdu la moitié !

Reprenons plus lentement pour les décérébrés mentaux (ou pour ceux qui ont arrêté leurs études avant la 6ème … les demeurés mentaux quoi) en utilisant une figure simple: le rectangle.

Bof... c'est pas très clair ! * « J'ai l'impression que c'est une demi-sphère à l'intérieur d'un rhombicosidodécaèdre à bords arrondis... ou alors c'est le dessin d'un oiseau représenté selon une coupe longitudinale au niveau de l'abdomen » dit le sous-doué.

C'est déjà mieux ! * « Ah il y a quatre angles droits... Bon sang mais si bien sûr: c'est forcément un rectangle ! Ou alors c'est un oiseau …. { 5 minutes plus tard } Mais qu'en est-il des longueurs des côtés ? » s'interroge le sous-doué … Mais peut mieux faire !

C'est maintenant que les versions divergent !

a) Choix du Mauvais Pédagogue

Le mauvais pédagogue pensera à tort que l'élève reconnaîtra aisément un rectangle en utilisant le codage suivant: Terrible erreur !!!

Cela mérite toutefois quelques précisions:

• Tirer un trait sur les côtés [AB] et [DC] aura pour effet de déstabiliser l'élève. En effet, « Tirer un trait sur quelque chose » signifie: « Oublier ; ne plus vouloir parler de ; ne plus s'intéresser à ; renoncer à » ce qui envoie un message contradictoire. Comment peut-on décemment penser intéresser un élève à la géométrie si on lui demande dans le même temps d'y renoncer ?

• Tirer deux traits sur les côtés [AD] et [BC] demandera à l'élève de commencer par tirer un trait sur chacun... Le malheureux les aura déjà oublié avant d'avoir terminé !

• Reconnaissons également que ces deux symboles sont quand même rudement proches visuellement. Il est fort probable que l'élève moyen finisse par en déduire que AB = BC = CD = AD, ce qui constituerait une effroyable confusion ! Je n'ose l'imaginer mesdames, messieurs cela me glace le sang, littéralement ! Vous rendez-vous compte ? Une telle confusion dans un jeune esprit fragile conduirait notre élève insouciant vers une vie marginale faite de délits mineurs. Quant à l'élève sous-doué... ouf mon Dieu c'est pas possible... cela en ferait un dangereux sociopathe complètement détraqué, un monstre de perversion ! Parfois une vie tient à peu de chose: un rectangle qu'on pensait carré et c'est déjà trop tard (il ne tournera plus jamais rond).

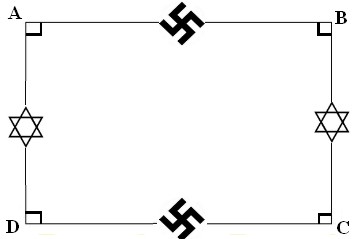
b) Choix du Bon Pédagogue

Le bon pédagogue quant à lui est nettement plus avisé. Il sait comment intéresser l'élève, comment impliquer l'élève dans son travail tout en le ménageant. Ce dernier lui évitera en effet toute confusion possible, il travaillera en toute sécurité comme en atteste la figure suivante:

« Ca me paraît limpide: AB = CD et AC = BD mais AB est différent de BC ! C'est un rectangle mais pas un carré !!» s'exclame avec fougue le sous-doué, presque étonné d'avoir compris ! (note: remarquez au passage que pour un sous-doué, il s'exprime sacrément bien ce con... sans vouloir me vanter !)

Utiliser ces symboles comporte les avantages suivants:

• Le professeur fait prendre conscience à l'élève que les matières ne sont pas cloisonnées. En utilisant la transversalité maths – histoire c'est alors l'occasion de rappeler à l'élève les atrocités commises par les nazis contre les juifs au cours de la seconde guerre mondiale et l'opposition Croix Gammée/Etoile de David n'en sera que plus évidente...

• Impossible donc de les confondre ! Difficile en effet au vu de ce qui vient d'être rappelé plus-haut.

• Enfin, nul doute que le petit juif au premier rang n'aura d'yeux que pour le professeur et que son attention sera la plus totale (à condition bien sûr que le petit gros antisémite derrière lui arrête de lui piquer le cou avec la pointe de son compas).

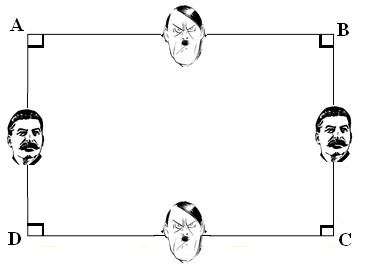
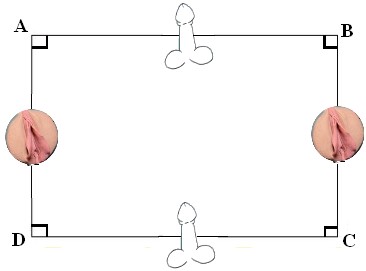
Il existe aussi d'autres variantes de codage qui sont tout aussi performantes, l'idée générale étant toujours d'associer deux symboles aux antipodes l'un de l'autre:

Sur votre gauche (et à droite) ce bon vieux Joseph, en haut (et en bas) le toujours très chaleureux Adolf

Y-a-t-il vraiment besoin d'expliquer le sens de ces symboles ?

Codages très utilisés dans les établissements catholiques

THE codage international... of course !

Ahh ce bon vieux Ribéry !

c) Ci-dessous quelques exemples de Codages à éviter absolument !!

Ils sont trop proches... bien trop proches !!

Ikéa c'est pas de la merde... quoique !

Hummm que c'est bon le bec de poulet frit !

Le couple de l'année: DSK - Naffisatouf... toujours aussi glamour ! Beaucoup trop proches !

Un costard : 3158 €, un salaire de premier ministre : 14 910 € brut / mois, avoir le charisme d'une huître : ça n'a pas de prix... Pour tout le reste il y a Jean-Marc Ayrault (ou pas !).

Les classiques pour la fin !

Cet article a une chance non nulle de figurer dans le Best Of ou de ne pas en être.
S'il vous a enthousiasmé, votez pour lui sur sa page de vote ! Ou pas.