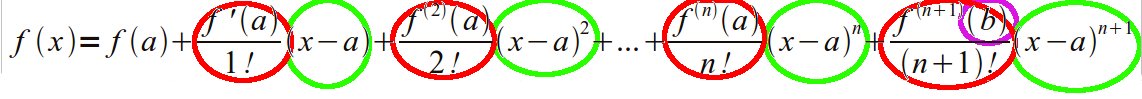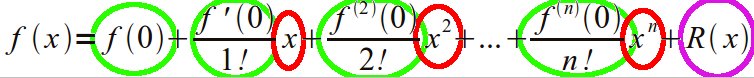Approximation
L'art de l'approximation consiste à obtenir des résultats presque justes là où on pourrait avoir des résultats justes. Il est utilisé essentiellement en médecine, en physique et plus généralement partout où l'erreur n'a aucune conséquence.
Étymologie et définition
Approximation: Du geek proxy, "relayeur, qui assure un lien", et du Serbo-Tchonque màttion, "rapport". Le tout avec un préfixe privatif a-.
La définition la plus cohérente et approximativement juste serait "qui assure un lien entre ce qui n'a aucun rapport". Néanmoins, il y a un certain lien entre l'approximé et l'approximation.
Les théorèmes du tailleur
Londres, 1712. Alors que la prostitution sous la pluie et l'alcoolisme sous la pluie constituent les principaux passe-temps, le projet Wikipédia commence à prendre forme. Ils ont réuni des administrateurs et des incultes (l'un n'empêchant pas l'autre), mais il leur manque deux choses essentielles : internet et surtout des informations vagues et incorrectes. Un des membres de ce projet était un anonyme que nous appellerons dans la suite de l'histoire le tailleur. On sait assez peu sur lui, si ce n'est qu'il était tailleur et qu'il n'avait pas de nom. Cet absence de repère identitaire avait provoqué nombre de pathologies mentales chez lui : un amour immodéré pour les mathématiques, le syndrome Gilles de la Tourette et une paranoïa excessive qui le poussait à vouloir tout savoir sur tout. Il exerçait donc son métier de tailleur et profitait de son temps libre pour trouver un moyen de transformer des informations précises en informations approximatives. Ainsi naquirent les formules du tailleur.
Théorème du tailleur-la grange
Il inventa la première alors qu'il comatait dormait dans une grange, comme tout bon londonien expulsé de la ville après une soirée arrosée. On dit que lorsqu'il découvrit la formule, il se leva du tas de foin brusquement en hurlant des incongruités, sortit nu de la grange, puis s'écroula dans son vomi sous la pluie.
En rouge les coefficients, en vert les polynômes et en violet moche les inconnues.
Cette formule utilise la notion de dérivée, c'est à dire qu'il faut laisser dériver l'information (ici représentée par f(x) ) le plus longtemps possible pour obtenir un résultat plus précis, mais plus tordu. On appelle cela une approximation à l'ordre n.
Elle permettait de traiter des informations de façon à avoir une approximation en termes polynomiaux tout simples et une erreur avec une inconnue, b, qui varie de 0 à a, bien dans l'esprit du projet mais encore trop précis.
Théorème du tailleur feat. McLaurin
Une grande avancée dans l'approximation fut réalisée quand le tailleur s'associa avec le rappeur écossais McLaurin. Leurs travaux se concentrèrent sur l'amélioration de l'aléatoire, sur la méconnaissance de l'erreur, sur le beat et sur les biatchs. Le résultat fut annoncé lors d'un grand slam à la Royal Bewery of Edinburgh.
En vert les coefficients, en rouge les polynômes et en violet moche les inconnues.
Ici, plus question de choisir le point de vue de l'approximation: tout est fait à partir de 0, ce qui assure une erreur éléphantesque dès qu'on s'en écarte un peu trop. La notion de reste inconnu permet de masquer complètement cette erreur et ainsi faire passer l'information approximée pour vraie.
Néanmoins, on connait toujours les coefficients de l'approximation qui sont de simples dérivées de l'information: le tailleur se fit copieusement latter fut gentiment prié par Wikipédia de revoir sa copie et de proposer plus approximatif et plus faux.
Théorème des développés limités
Après la tatane qu'il s'était prise, le tailleur décida de se muscler un peu, l'histoire de pouvoir se défendre face à la horde d'administrateurs impatients. Alors qu'il faisait quelques développés-couchés, un petit malin s'amusa à rajouter du poids sur ses haltères. Ses bras lâchèrent sous les 35kg de fonte et la lourde barre de fer lui comprima le thorax. Pendant que son cerveau manquait d'air, il eu la révélation de la formule ultime:
En vert les polynômes et en violet moche les inconnues.
Une merveille: les coefficients a1, a2, a3, etc. sont tirés aux dés et le point a est de retour pour permettre des erreurs de calcul plus nombreuses. L'approximation n'a plus rien à voir avec l'information approximée, et le reste est toujours totalement inconnu. Le tailleur présenta son théorème à wikia sous le nom des "développés illimités", car il était possible de créer un nombre infini d'articles tous plus faux les uns que les autres à partir du même sujet, mais les admins ne disposant que de dés à 6 faces, il fut renommé "théorème des développés limités".
La mort du tailleur
Le tailleur avait fait une découverte majeure dans le domaine de la désinformation. Les dons, récompenses et autres back-chiches affluaient. Il aurait pu conduire des caisses approximativement grosses et se faire des femmes approximativement bonnes, mais il sombra peu à peu dans la folie. Il se mit en tête de découvrir qui il était réellement. Il utilisa tous les moyens à sa disposition : méditation, cocaïne, prière, quizz Facebook, etc... Mais rien ne marcha. De dépit, il décida d'utiliser son premier théorème sur lui-même quitte à ne trouver qu'une approximation de lui même.
Il s'embarqua donc sur un radeau au beau milieu du Pacifique. Il dériva pendant des jours et des jours. Au fur et à mesure, il trouvait les réponses approximatives à ses questions les plus profondes : Qui suis-je ? Où cours-je ? Dans quel état j'erre ?
Il mourut avec ses compagnons de méditation au bout du 13e jour, avalé par un cachalot alors qu'il avait découvert le sens de la vie.
De la dérivée
Le principal problème des formules du tailleur est que tout ne peut pas être mis sur un radeau, et les conditions de dérivation sont très dures. Danger, faim, soif, cachalots, tout cela est monnaie courante pour ces aventuriers, et une dérivation ne se fait pas sans une préparation physique minutieuse. Cependant, l'invention d'internet, d'IRC et des forums permit une véritable démocratisation de la dérivée. Chacun a pu laisser un sujet sur le net et le récupérer quelques heures plus tard complètement dérivé et prêt à être utilisé dans les formules du tailleur.
Exemples
Théorème du tailleur-la grange
Faites attention !
Cette approximation présente une anomalie à l'ordre 69.
|
Théorème du tailleur feat. McLaurin
Faites attention !
Cette approximation présente une anomalie à l'ordre 666.
|
Théorème des développés limités
Les équivalents et les négligeables
Équivalents
Un autre axe de la recherche d'approximations est la théorie des équivalents. Le principe est simple: si ce que l'on doit approximer peut être remplacé quelque chose de plus simple à étudier, alors il faut le remplacer.
Exemple
Négligeables
Le principe est aussi de simplifier ce que l'on a à étudier. Il faut repérer l'élément le plus important et éliminer tous les éléments plus petits que lui. Les éléments négligés sont tous rassemblés dans une seule expression : o, ce qui nous donne un résultat de la forme f(x)+o(f(x)).
Exemple
On remarque bien que le choix de l'élément le plus important est capital. Et quoi de plus important que le fourbe qui se planque derrière le drapeau ?
Remarques
- Cet article est approximativement déjà dans le best-of.
- Le kévin est un o de la langue française.
- Il ne faut pas confondre incertitude et approximation : l'incertitude est involontaire, elle !
S'il vous a enthousiasmé, votez pour lui sur sa page de vote ! Ou pas.