Théorème d'espérance de l'utilité

« Il y a des chances que ce que vous allez lire vous sera un jour utile. »

~ Sacha Guitry

« J'ai une colique d'estomac. Je suis venu ici dans l'espoir de trouver un remède. »

~ Paul Binocle

Vous ne serez pas déçus, Messieurs. Le théorème d'espérance de l'utilité exprime une propriété du comportement d'un agent économique rationnel face à un choix entre une alternative risquée et une alternative certaine dans la perspective de gains monétaires. Il a été fondé par Daniel Bernoulli, John Von Neumann, Oskar Morgenstern, H. Markowitz, William Sharpe, M. Friedman, L.J. Savage, L.S. Shapley, John Nash, James H. Miller, dans le cadre de la théorie des jeux. La pléthore de contributeurs s'explique simplement par le besoin de s'amuser. Mais ce n'était pas très amusant au final, d'où la théorie des jeux.

	La nana aux cheveux bleus dit :
	Chouette programme de grandes écoles en perspective !

Le paradoxe de Saint-Pétersbourg

Tout ce petit beau monde se pencha sur la question en même temps. Ouais, comme toi en ce moment, parce que la question était écrite en tout tout petits caractères. Au fait t'arrive à cliquer sur ce p'tit lien ?? Ce serait marrant à ce niveau microscopique.

	La nana aux cheveux bleus dit :
	Ça y est Lascaux, j'ai mis mes lunettes ! Je suis prête pour la leçon ! J'suis mignonne hein ? Mince t'écris drôlement gros !

Grrrmmpppffff.... maintenant tout ce petit beau monde connaît mon nom puant à chier dans une grotte. Je sais pas si j'aurai la force de continuer. Bon, je continue.

Soit le mendiant de Saint-Pétersbourg. Il détient un billet de loterie de 20 € lui donnant à coup sûr la possibilité de gagner 1000 € avec une probabilité de 50 %. Tout à coup quelqu'un — son père, admettons — vient lui proposer de racheter son billet 1000 €. Avec ces 1000 €, il peut acheter (pouvoir d'achat ! pouvoir d'achat ! je t'ai repéré attention à ton cul !) 50 billets de loterie équivalents à celui qu'il détient, mais ce n'est pas sûr que le bar-tabac du coin en ait encore 50 à vendre.

Devant la certitude de gagner 1000 € avec une probabilité de 50 % et l'incertitude de gagner 50 fois 1000 € avec une probabilité de 50 %, que choisira le mendiant ?

Bon je crois que c'est pas clair... je reprends.

	La nana aux cheveux bleus dit :
	Pourquoi il garderait pas les 1000 € ? Il échange le risque du gain de 1000 € contre une certitude de gain de 1000 €.

Ah oui c'est ç... ben c'est exactement ce que j'allais dire. Ne m'interromps pas ! Tu te crois où ? Dans un coitus interruptus ?? Un peu de retenue voyons !

Hmm donc le mendiant a le choix entre 1000 € incertains et 1000 € sûrs. Arrangeons ces alternatives dans une matrice (les probabilités sont en base 1 — i.e., une probabilité de 1 = 100 % de chance) :

Alternative risquée		Alternative certaine
Gain	Probabilité	Gain	Probabilité
1000 €	0,5	1000 €	1
0 €	0,5

« Mais voyons ! » : Oskar Morgenstern a lu et désapprouvé la tournure que prend le texte.

Putain mais montré aussi joliment, le choix est évident. Qu'est-ce que c'est con comme base de théorème... J'aurais pu le deviner, et en plus j'ai pas un nom con comme Bernoulli à laisser à la postérité.

Qui c'est le petit con qu'a écrit ça ??

Le retour du paradoxe de Saint-Pétersbourg de Daniel Bernoulli

Donc Daniel — ô monde impitoyable — prédit que le mendiant choisit les 1000 € sûrs.

	La nana aux cheveux bleus dit :
	Je vois pas le paradoxe. Le choix me semble tout à fait rationnel et libre de contradiction.

James H. Miller trouve cet article scientifique fort louche.

Normal, il n'y en a pas. Bernoulli disait : « Ouais le paradoxe, c'est que le mendiant normalement il est trop con pour accepter l'offre. Sinon il en serait pas à balayer les trottoirs avec ses pieds. » Et pis tu sais en quoi il était fait le cerveau de Bernoulli ?

	La nana aux cheveux bleus dit :
	Euuhh... en nouilles ?

Voilà. Putain t'as lu mes fiches avant de venir en cours ?

Ma fiche de cours. Faudrait que je pense à la cacher plus soigneusement.

L'espérance mathématique et utilité

Le vrai problème... C'est que certains ont fait la confusion entre utilité et espérance mathématique. Ces notions sont totalement différentes. L'utilité d'un gain risqué n'est pas trivialement équivalente à l'espérance mathématique de ce gain.

Définition de l'espérance mathématique

Bon pour la petite note : l'espérance mathématique exprime le gain espéré "en moyenne" d'un tirage aléatoire de nombre. Mais les coefficients de pondération de cette moyenne viennent de la distribution de probabilité des différentes possibilités.

Soit un dé à 457 faces numérotées de 1 à 457. Le lancer de dé m'octroie la somme en euros égale au numéro de la face résultante. Bien entendu, chaque face est équiprobable à exactement ${\frac {1}{457}}$. L'espérance mathématique du dé $E_{de}$ correspond donc ici à la moyenne ${\overline {E}}$ :

$E_{de}={\frac {1}{457}}\times 1+{\frac {1}{457}}\times 2+...+{\frac {1}{457}}\times 457={\frac {1+2+...+457}{457}}=229={\overline {E}}$

L.S. Shapley ne voit que trop bien où mène le concept d'encyclopédie libre.

Mon espérance de gain est donc de 229 euros.

À présent soit un dé pipé. Une face va peser relativement plus que les autres, disons la 266^e, à la probabilité $65/457$. On s'attend alors à une espérance de gain légèrement supérieure car 266 est au-dessus de la moyenne 229. On a maintenant :

$E_{pipe}={\frac {1}{457}}\times 1+{\frac {1}{457}}\times 2+...{\frac {65}{457}}\times 266+...+{\frac {1}{457}}\times 457=266,25>{\overline {E}}$

La nana aux cheveux bleus va ici faire une remarque sans intérêt et je vais lui rabattre le caquet. Vous verrez, ça sera cool.

	La nana aux cheveux bleus dit :
	Eh, la somme des poids fait plus de 100% !

Et alors ? T'as déjà vu un dé de 457 ? Qu'est-ce qui te dit que c'est pas un dé de 457 qui t'a créé à partir de sel et de poivre ? Alors la ferme ! Je disais donc... L'espérance mathématique est donc une notion extrêmement compliquée, avec laquelle les biologistes ont notamment tenté d'expliquer l'existence de l'ornithorynque.

Relation avec l'utilité

Retournons à la situation initiale du paradoxe de Saint-Pétersbourg, que voici :

Alternative risquée		Alternative certaine
Gain	Probabilité	Gain	Probabilité
1000 €	0,5	1000 €	1
0 €	0,5

Évaluons avec de nouvelles données :

Alternative risquée		Alternative certaine
Gain	Probabilité	Gain	Probabilité
1000 €	0,5	1200 €	1
0 €	0,5

H. Markowitz a soudainement envie de pleurer.

Cette fois c'est sûr, le mendiant s'en fiche, il va continuer à prendre l'alternative sûre, mais à 1200 € cette fois. Et là ?

Alternative risquée		Alternative certaine
Gain	Probabilité	Gain	Probabilité
1000 €	0,5	2154577 €	1
0 €	0,5

Pareil. Allez un petit piège, parce que bon.

Alternative risquée		Alternative certaine
Gain	Probabilité	Gain	Probabilité
1000 €	0,5	999,99 €	1
0 €	0,5

Bien sûr il va continuer à... AH ! N'allais-je pas me prendre à mon propre piège HAHA ! Vous ne commettrez pas la même erreur hein ! Là, le mendiant hésite ! Forcément, il compare avantageusement 1000 € à 999,99 €, et va donc privilégier l'alternative risquée !

L.J. Savage est écœuré.

Or, quelle est l'espérance mathématique de l'alternative risquée ? Elle est exactement de 500 € (c'est exactement la moyenne des deux possibilités de gain). Qu'on choisisse l'alternative risquée ou l'alternative certaine, 500 € c'est toujours inférieur à 2 154 577 € ou 999,99 €. C'est un mauvais discriminant, c'est une variable qui statistiquement parlant n'explique pas le comportement du mendiant. C'est donc bien une notion extrêmement compliquée, d'autant plus qu'elle ne sert strictement à rien.

La somme des 1000 € s'appelle l' équivalent certain, car il a la forme X00...00, i.e., un chiffre X non zéro suivi de N zéros. C'est à ça qu'on reconnaît une somme "certaine".

L'équivalent certain est très nettement à droite.

D'après ce qui vient d'être dit, l'utilité de l'espérance E, notée $U(E)$ est donc nulle, quelle que soit E.

$U(E)=0$

C'est pourquoi parler d' utilité de l'espérance ne veut absolument rien dire. Or, la nullité de l'utilité de l'espérance implique aussi la nullité de toute espérance d'utilité, car on a :

$E(U(E))=E(0)=0$

Ce que tout ça veut dire, c'est qu'un mendiant n'a besoin que de... comment on appelle ça déjà... euh... je m'en souviens jamais de ce truc...

	La nana aux cheveux bleus dit :
	Le bon sens !

Ta gueule ! Ouais, le bon sens !!! Il a besoin que de ça pour faire des décisions d'investissement rationnelles, et se passe volontiers d'outils mathématiques de frimeurs.

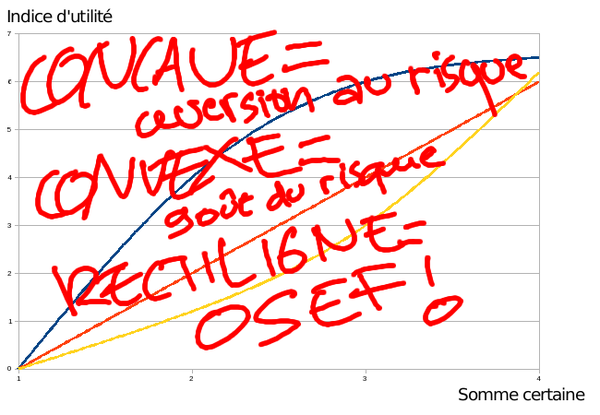
Le théorème d'espérance de l'utilité

Axiomes

William Sharpe a du mal à croire ce qu'il lit. Ça lui donne envie de vomir.

Les axiomes forment la phase la plus simple. Cette section devrait donc couler de source. Les axiomes expriment seulement les hypothèses de base qui conditionnent le domaine d'applicabilité du théorème. Il suffit de les admettre et en tirer notre théorème qui nous vaudra un petit Prix Nobel de l'économie. IL SUFFIT DE LES ADMETTRE, GÉNIAL NON !!!

Les axiomes sont les suivants :

1. La Lune s'est écrasée sur la Terre, plus précisément sur le Pont d'Avignon où tout le monde il y danse tous en rond. L'espèce humaine n'existe donc plus, emportée dans la déflagration.
2. La Terre est ronde, et non ovale aplatie aux pôles.
3. L'espace est notre dépotoir et devrait résorber tous nos déboires en matière de stockage des déchets.
4. Les mammouths n'ont pas fait long feu pendant la Grande Ère de Glaciation.

	La nana aux cheveux bleus dit :
	Mais c'est pas ça !

Bien sûr que c'est pas ça ! Bien sûr que je raconte des conneries et pas toi ! Connasse !

Donc, ouais, c'était pas ça. Les VRAIS axiomes, ceux qui font autorité dans le milieu, sont les suivants :

1. Complétude
2. Transitivité
3. Continuité

La complétude, c'est que le mendiant sait toujours classer les situations par ordre de préférence. Il n'est jamais coincé. Et quelqu'un de jamais coincé est toujours complet, tout le monde sait ça.

La transitivité, c'est le fait que si le mendiant préfère A à B et B à C, alors il préfère A à C.

La nana aux cheveux bleus dit :

Ouais mais regarde ce plan avec 3 villes A, B et C : Supposons que mon critère de choix entre 2 villes soit en 2 parties : (1) s'il y a un chemin de fer à sens unique entre les 2 villes, je préfère la ville à partir de laquelle je peux rejoindre l'autre en train et ainsi faire coup double ; sinon, (2) s'il n'y a pas de chemin de fer, mon critère classique c'est la distance. Certes je préfère A à B et B à C à cause de la distance, mais entre A et C, je choisis C plutôt que A, car je peux rejoindre A en train à partir de C. La transitivité ne s'applique donc pas.

Oups le coup est parti tout seul.

	La nana aux cheveux bleus dit :
	Ppppffffff

Cela me dérangerait-il de poursuivre ? Non. Alors je poursuis. La con...

	La nana aux cheveux bleus dit :
	La con...

... ti....

	La nana aux cheveux bleus dit :
	ti...

... nui....

	La nana aux cheveux bleus dit :
	Mais j'ai rien fait. Je faisais que répéter car à chaque fois je me ramasse une paire de mandales !!

Ouais mais là fallait juste pas l'ouvrir même si c'était juste pour imiter les porte-jarretelles sur un gnou femelle en rut.

Donc je répète. La transitivité, c'est le fait que si le mendiant préfère A à B et B à C, alors il préfère A à...

	La nana aux cheveux bleus dit :
	Aïe.

John Nash crache sur cet article.

Ça t'apprendra à ne rien dire rien que pour me donner tort. La transitivité, c'est le fait que si le mendiant préfère A à B et B à C, alors il préfère A à C !!! Ce genre de raisonnement en triangle tient tout seul.

 

 

	La nana aux cheveux bleus dit :
	Lascaux.

Quoi ? QUOI ???

	La nana aux cheveux bleus dit :
	J'ai perdu mon œil.

Et alors ??? Joue au yoyo avec, sérieux arrête de me faire chier MERDE QUOI !

Putain ça commence à me faire sérieusement disjoncter cette affaire. Putain mais on en est qu'aux FONDATIONS, aux AXIOMES, et j'arrive pas à avancer ! Faut arrêter 2 secondes avec les contre-exploits, les désenchantements des dragons et la fontaine de sénilité des Bahamas ! Mais tu crois que c'est quoi un théorème ?? « Avec la cape de Superman, si je saute je m'écrase par terre » ??? Mais ce n'est ni un énoncé de théorème ni un lemme, c'est un putain de malheureux lemming ! Ah tiens tu veux ton "théorème" de l'utilité, sans approche pédagogique et tout le cassage de cul qui va avec ???

TIENS VOILÀ TA FLAQUE DE THÉORÈME !

Théorème de l'espérance de l'utilité — L'utilité d'un gain est égale à l'espérance TIRELI PIMPON PIMPON mathématique des utilités des SIYAHAMBA KUKHENYENI KWENKHOS sommes monétaires possibles.

Tiens tu voulais ton graphe de courbe ?? TU VOULAIS TON GRAPHE DE COURBE ??????????

John Von Neumann n'a pas reconnu son théorème.

MOI J'ME CASSE !!!!!! J'PARS À SAINT-PÉTERSBOURG ! J'VAIS M'ACHETER UN BILLET DU LOTO LOCAL ET LE REVENDRE AU PRIX DE LA CAGNOTTE ! LÀ-BAS ON M'COMPRENDRA !

* VLAN ! *

	La nana aux cheveux bleus dit :
	Snif.

Notes

Daniel Bernoulli dit : « Il faut faire quelque chose, et rapidement. La désencyclopédie ne peut pas survivre avec un tel caractériel aux commandes. La nana aux cheveux bleus elle-même ne va pas durer très longtemps à ce rythme là. À quoi cet auteur d'articles va-t-il encore s'attaquer ? Je crains le pire ! »

« Encore ! Encore ! »

~ Paul Binocle à propos de ne plus avoir la colique

Portail de Picsou

Cet article a failli être élu au Best Of de la Désencyclopédie.
Si vous l'avez adoré, vous pouvez encore relancer le débat.