Critique de la raison pure
La Critique de la raison pure (Kritik der reinen Vernunft) est un ouvrage "coquille" maçonné par Emmanuel Kant, entièrement basé sur une erreur typographique.
Concept de critique de la raison
Avant tout un auteur raté, Kant a misé sur une approche critique de sa discipline. Certes, la conjoncture faisait que le philosophe écossais David Hume avait déjà eu raison et faisait l'unanimité. Mais la même conjoncture est assez conne, car elle allait aussi voir la naissance de la critique des hommes qui ont raison et font l'unanimité. À la lumière de ce miracle séculaire, Hume s'était donné tort lorsqu'il soutint la thèse selon laquelle « tout miracle ne peut être certifié que par une preuve proportionnellement extraordinaire. » Juste une extraordinaire désinvolture intellectuelle de la part du critique est nécessaire.
À l'analyse, l'expression "critique de la raison pure" cache beaucoup plus de sens qu'il n'y paraît. Heidegger l'avait le premier souligné dans sa rétrospective kantienne du XIXe : la "critique de la raison pure" est paradoxale si l'on entend une critique contre de la raison. Or comment attaquer un penseur qui a raison ? Au contraire, la critique appartient à la raison elle-même qu'on préfèrera la plus pure possible. La "critique de la raison pure" se lit donc comme une "critique en provenance de ma raison qui est pure". De ce point de vue, la Critique se range, comme le Coran et les lettres ummites, parmi les écrits non-humains.
Conception
Auteur d'une Histoire de l'Empire britannique, Hume a naturellement inventé l'empirisme britannique. Cette école de pensée implique une nouvelle manière impériale d'envisager la connaissance, à savoir que tout ce qu'on connaît est assuré par nos sens défaillants et malades, au chevet desquels doit accourir le principe de l'induction. Rien n'est sûr et vérifiable à 100%, mais Kant l'ajuste à la condition si l'on se base sur l'expérience et le vécu. Car Kant part lui d'un postulat pur à 100% :
- A priori, Dieu existe
Il tape alors répétitivement du poing dans son autre main :
Heureusement, Kant tombe sur le lapsus fondateur de l'idéalisme germanique. En effet, l'Homme n'a aucune connaissance empirique de Dieu. Or, en allemand, "aucun" se dit "kein", et comme les r Kant les tourne gauchement comme les k, cela donne que son éditeur lit "rein" (= pur) au lieu de "kein". Vient alors le prétexte précepte fondamental de la théologie transcendantale : l'Homme a une connaissance pure de Dieu. La confusion typographique positionne la Critique comme un modèle d'ouvrage coquille.
Tout ce qui est "a priori" sera donc pur au-delà de l'expérience et des connaissances empiriques. La raison kantienne sera pure, et jouira de la position privilégiée de la critique facile.
Les fondements du système kantien
Propositions analytiques et synthétiques
Dans une proposition analytique, le sujet contient entièrement le prédicat. On parle alors de sudicat. Dans Dans l'incroyable monde des sudicats aux collections Collections du jardin, Aristote tire de la proposition
- Le sudicat contient entièrement le prédicat
qu'il y a un sudicat, le sudicat, et son prédicat contient entièrement le prédicat. Plus remarquable, dans la tautologie
- Le prédicat est un sudicat contenant entièrement le prédicat
le prédicat est un sudicat, et ce sudicat est le prédicat contenant entièrement le prédicat. Tout est donc à la fois prédicat et sudicat se contenant soi-même.
Malgré la valeur de ce résultat de symétrie linguistique ─ non moins intéressant qu'une dissymétrie moléculaire de Louis Pasteur par exemple ─, Kant qualifie les connaissances analytiques de « peu intéressantes ». Les post-kantiens attribuent ce snobisme au survol probable du fantastique 52e chapitre. Le Grec y fige l'art de concilier ses passions du jardinage et de la logique du premier ordre en attribuant à chaque nain de jardin un petit sudicat. Ainsi pour son propre potager associe-t-il son plus petit nain de jardin à
- Les grenouilles ressemblent étrangement aux martiens
et son plus grand à
- L'éléphant a deux énormes bites
propositions qu'il qualifie « de premier ordre ».
À l'opposé, le prédicat d'une proposition synthétique est hors sujet, ce que Kant trouve « intéressant et croustillant », car ce principe fonde l'illusion dialectique et surtout les énigmes les plus coriaces. Le Sphinx par exemple se vautre dans ses tournures aristotéliciennes :
- Quel être, pourvu d’une seule voix, a d’abord quatre jambes, puis deux jambes, et trois jambes ensuite ?
Au lieu de quoi, il aurait dû poser à Œdipe une colle synthétique :
- Quel être, pourvu d’une seule voix, a 9 pattes ?
La note synthétique de la question aurait échappé au thébain ─ i.e., le simple fait que chaque patte puisse se rapporter à une maturité différente du sujet. Il aurait alors balbutié : « Ben euuuuh...... un tuyau de jardin ? Euh non !! Une pochette de crayons de couleur ? Nan c'est nul, ça peut trop pas être ça ! Allez dernière chance ! Fais pas ton con ! » Là le Sphinx l'aurait bouffé.
Les mathématiques pures
L'expérience véhicule de nombreuses données erronées. Il est courant d'y croiser des lignes droites épaisses et des triangles dont la somme des angles fait plus de 180 degrés, ce qui a suscité maints rires polis de la gente idéaliste allemande. La vraie vie tend aussi à susciter des propositions analytiques décevantes. Par exemple, la proposition
- L'arithmétique est incomplète
tirée du théorème d'incertitude de Gödel, est parfaitement analytique, car l'incomplétude est inhérente à l'arithmétique.
Les mathématiques pures ont ceci de huileux que l'intuition mathématique est hydrophobe à pareilles aberrations. Et en particulier l'intuition de l'axiome du choix, car après avoir converti l'élève via une autre science, la physique, celui-ci a généralement une intuition pure et a priori de sa discipline.
Mais comment l'intuition mathématique peut-elle être a priori ? Déjà, intuitivement, le nouveau-né sait compter sur sa mère, c'est un robuste arithméticien. Les babillages qu'il produit avec sa bouche sont au moins aussi inintelligibles que les preuves méta-mathématiques de Gödel. Par exemple, dans la vidéo plus bas, l'enfant fait la lecture à voix haute du passage suivant de l'article Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme de Gödel :
| Pour déduire le second théorème d'incomplétude des trois conditions de Löb, il suffit de reprendre le raisonnement déjà fait ci-dessus. Soit G la formule de Gödel construite pour la théorie T, qui, si cette dernière est cohérente, entraîne ¬DemT(⌈G⌉). D'après D1 et la cohérence de la théorie T, G n'est pas démontrable dans T (premier théorème). On formalise maintenant ce raisonnement dans T. Supposons que dans T, DemT(⌈G⌉). Comme, d'autre part, on démontre dans T que DemT(⌈G ⇒ ¬DemT(⌈G⌉)⌉), on déduit par D3 dans T, DemT(⌈¬DemT(⌈G⌉)⌉). Finalement, par D'3, on a montré ¬cohT dans T. Récapitulons : on a montré dans T que DemT(⌈G⌉) ⇒ ¬cohT, c’est-à-dire par définition de G, ¬G ⇒ ¬cohT, et par contraposée cohT ⇒ G. Or on a vu que G n'est pas démontrable dans T, donc cohT n'est pas démontrable dans T. |
Or l'espace participe, comme l'ensemble des mathématiques pures, de l'intuition a priori. Ce n'est pas une donnée empirique biaisée par l'expérience. Évidemment, souligne Kant, le fameux espace vide n'est pas une donnée de l'expérience, mais l'intuition a priori d'une chose inexistante.
Chose inexistante ? Ou je suis fou, ou nous avons bien là une proposition synthétique. La chose en soi peut être exactement définie quand bien même elle n'existerait pas ; on peut même la définir comme n'existant pas. Voilà, dirais-je, le dernier ingrédient essentiel qui faisait défaut à notre édifiant croustillant de légumes ! (...)
|
||
—Emmanuel Kant | ||
En corrolaire, nos sens, en particulier le sens de l'espace, sont baignés dans une ignorance intuitive[1]. L'ignare intuitif par excellence ─ le bébé ─ n'aura jamais la notion sensible d'espace vide, même jeté de la fenêtre la plus élevée possible.
Les relations mathématiques
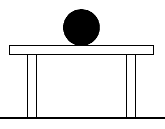
Dans le figure suivante, le ballon est-il sur la table ?
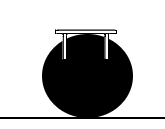
Réponse : non. C'est une illusion d'optique créée par l'opacité de l'image et le taux de pénétration nul de nos rétines. En fait c'est le ballon qui porte la structure intégrale de la table :
En revanche, les relations mathématiques sont absolument nécessaires. Il est de raison que le nombre 3 est juste sur le nombre 2, le nombre 4 sur le nombre 3, etc. Ce sont bien des nombres rationnels. On concède a priori que la science des nombres est infiniment plus sûre et nécessaire que la stabilité de n'importe quel bâtiment humain. En comparaison, une pyramide tombe aisément sur le côté ; l'instabilité empirique va induire un nouveau basculement et ainsi engendrer un roulement perpétuel contraire à l'intuition a priori. Seuls les roms noteront la stabilité dans l'instabilité, férus de philosophie germanique qu'ils sont[2].
L'esthétique transcendantale
À l'ère pré-kantienne, la philosophie n'a toujours pas solutionné le paradoxe des jumeaux. En leibnitzien, si les jumeaux sont égaux en tout point, ils sont la même chose dans l'absolu. Comment se sortir de ce chosisme unifié sans recourir à l'empirisme ? Les sophistes grecs se prononçaient déjà sur la question.
(i) Les jumeaux se ressemblent comme deux gouttes d'eau.
(ii) Les gouttes d'eau sont donc aussi des jumeaux.
(iii) Comparons un jumeau et une goutte d'eau. On constate bien que ces jumeaux sont différents. CQFD
Variations possibles de (1) (les développements sont laissés au lecteur perplicaxe) :
- Les jumeaux sont identiques au poil de nez près
- Des jumeaux sont sur un bateau
- Huit jumeaux sont en finale du 100 mètres
- Deux jumeaux sont en finale de Roland Garros 2003
- Je lâche mes bébés jumeaux par la fenêtre en même temps
La preuve est faible, car analytique. Pour éviter l'écueil analytique, Kant produit un énoncé transcendantal que confirment les plus récentes recherches en biologie expérimentale appliquée aux rats pré-sevrés. Il part de l'intuition a priori de l'espace :
L'homme conçoit la multiplicité dans l'espace par le pouvoir de synthèse a priori de son imagination productive. Sa science innée de la géolocalisation lui permet de se repérer dans le vide, qui, pour lui, se navigue plus tel un océan tranquille que telle la mer déchaînée ballottant le humble marin en quête du sol ferme de l'île de la raison.
|
||
—Kant | ||
Sa démonstration des gros morceaux de l'espace anticipe de 1 siècle le microscopisme de Christopher Alexander, le courant dominant actuel.

La dialectique transcendantale
Aussi pure que soit l'intuition, elle est d'une manière ou d'une autre liée aux sens malades de l'Homme. Descartes disait souvent : « J'ai l'intuition que je me trompe. » Et Blaise Pascal que « l'erreur était intuitive chez les Jésuites, les casuistes et les molinistes. »
Un Homme dont l'entendement est porté par les sens a une nette tendance à l'erreur et à l'oubli. Qu'il tombe sur un "cheval vertueux", et le voilà qui en perd son latin. Kant relève le cas de Hume et sa difficulté à ne pas confondre les locutions latines a priori et a posteriori. Ironiquement, la notion d'habitude au fondement de sa loi de causalité fonctionne mieux avec une causalité a priori qu'avec une causalité a posteriori, car l'on s'habitue plus efficacement à quelque chose qui nous est donné a priori, c'est-à-dire un peu à l'avance.
Au-dessus des sens, la raison pure est le siège des connaissances synthétiques a priori sans aucune réalité, donc décorrelées de l'expérience en leur fondement, et donc mais vraiment complètement pures, car « ce ne sont que des idées. » La difficulté du fameux "cheval vertueux" en tant qu'inexistant doit beaucoup à l'hypothétisation des connaissances "par design" ─ j'imagine quelque chose, donc je suis dans l'hypothèse. Kant lui oppose l'hypothétisation "par Dasein" ─ je dois hypothéser quelque chose, donc je la synthétise. Il construit ainsi toute une éthique transcendantale autour d'un "Dieu cheval vertueux hennissant" caractérisé "par Dasein".
Les idées cosmologiques
Kant, le premier, a noté que les connaissances synthétiques pures adoptent a priori la forme thèse / anti-thèse / synthèse. Chaque partie est a priori et obéit uniquement aux lois de la raison pure. On peut ainsi poser, en termes dialectiques, l'antinomie suivante :
- L'univers est infini → Thèse
- L'univers est fini → Anti-thèse
- L'univers est à la fois fini et infini → Synthèse
La première proposition voit l'univers comme une boîte. Si l'on sondait les limites de cette boîte, on s'apercevrait que cette boîte est en fait contenue dans une autre boîte qui serait vraiment l'univers, et ainsi de suite. L'univers est donc une boîte infinie. En même temps, c'est une boîte. Donc elle est aussi finie. Il vient que la notion d'univers à la fois fini et infini est une connaissance synthétique a priori, car elle allie deux propositions a priori (la thèse et l'antithèse) contradictoires.
Structure
La critique de la raison pure affiche une structure transcendantale fondée sur la table des matières. Pour ce faire, elle s'appuie sur la technique de l'ellipse de l'objet.
L'ellipse de l'objet
À la base, l'ellipse de l'objet va consister à couper les compléments d'objet dans une proposition.
Vimel prena.[3]
Esteban apportit.[3]
Nemo s'asseya sur.[3]
La figure de style enlève l'objet pour mieux coller au sujet. Ici il importe peu de savoir si Nems s'est assis sur un pot de colle, un bébé ou Ben, tant que Nemo s'asseoit sur. Il importe juste qu'on colle mieux au sujet[4].
Dans la théorie de la connaissance, l'ellipse permet d'élaguer une démonstration intuitive de ses développements superflus. En effet, pour faire admettre une démonstration ridicule, il suffit d'en soustraire les éléments ridicules. Soit la démonstration :
- L'univers est infini car c'est une boîte contenant toutes les boîtes imaginables
- L'univers est fini car c'est une boîte
- L'univers est donc à la fois fini et infini
L'utilisation astucieuse de la locution etc nous sortira d'un monde d'embarras :
- L'univers est infini etc
- L'univers etc
- L'univers est donc à la fois fini et infini
La table des matières
L'ouvrage entier est en fait une table des matières en 4 parties. Elle se présente sous forme d'un réseau de 4 "catégories" :
Qualité
Modalité
La raison pure ne répond que des notions les plus générales, les catégories, concepts purs illustrés principalement par la Conception Immaculée de Jésus Christ et, de manière plus "catégorique", le vagin de la Vierge Marie luisant fraîchement du foutre de nom de Dieu.
Le développement concret de cette table est renvoyée à l'autre ouvrage coquille Critique de la raison subtile (Kritik der feinen Vernunft). En superposant, à l'initiative du Cercle Viennois, les 2 ouvrages, on obtient :
Dans une présentation classique, la table des matières kantienne se distingue de la classique par le remplacement des renvois de page par des X, voire des hyperliens pour la version web 2.0. X dénote la multiplicité de la pagination et représente notre connaissance a priori de la page. Comme le numéro de la page dépend de l'expérience ("dans quel livre suis-je ?"), on ne peut a priori que connaître la page dans l'absolu, dans le cadre de l'expérience en général. Aux accusations de verbiage, Kant a donc fait valoir le caractère hautement "sommaire" de son œuvre :
Table des matières
|
Critiques et réception
Ce sont surtout les siennes en fait. Il les a principalement formulées à l'encontre de l'« l'hydre à deux têtes », à savoir John Locke[5] et son copain David Hume[6] qu'il a très mal reçus tout en les pardonnant en grand seigneur qu'il était.
La proposition fondamentale de Hume selon laquelle toute la connaissance humaine serait empirique contrairement à celle des melons[7], ne soutient justement pas le test l'expérience. Hume soutient en effet que la trajectoire de 2 boules de billard entrant en collision ne peut être prédite a priori et doit être révélée par l'expérience. C'est que dans l'esprit, il est tout aussi concevable que les boules entrent en contact et deviennent soudainement immobiles que si elles s'entrechoquaient et se repoussaient.
Au contraire, enchérit Kant, le problème avec l'expérience, c'est que les boules de billard « restent justement parfois collées l'une à l'autre; j'ai fait l'expérience à la maison ! » L'expérience est pleine de ces erreurs inintelligibles, inclus le comble du fait qu'on ne trouve aucune trace directe de Dieu.
Nous savons tous que la boule de billard de billard n'est pas une sphère parfaite. L'expérience montre que sur une surface horizontale plane, elle ne bouge pas si personne ne la touche. Et pourtant les imperfections font qu'elle devrait pencher d'un côté ou de l'autre et entrer en mouvement perpétuel. L'expérience est une fois encore en contradiction avec elle-même. Quant aux frottements, on ne me fera pas admettre qu'une "force de frottement" naisse "comme ça" juste pour annuler exactement la force de roulement de la boule. Des forces jaillissant ex nihilo sans aucune raison n'ont pas leur place dans une philosophie transcendantale. Dieu ne joue pas avec les boules de billard, que je sache.
|
||
—Emmanuel Kant | ||
Notes
- ↑ Kant se marre bien dans sa tombe quand tu fais passer l'intuition pour le "sixième sens".
- ↑ Oh ça casse du romanichel là MDR
- ↑ 3,0 3,1 et 3,2 Le lecteur notera que l'ellipse de l'objet ne prémunit pas contre les fautes de français.
- ↑ L'hypothèse du pot de colle part donc avec une longueur d'avance, contre toute attente.
- ↑ Kant : « Le Locke Ness, l'homme qui créait des mirages avec le bâton de la science. »
- ↑ Kant : « La Locke Humaine, le type qui se raccrochait au porte-manteau de la science empirique. »
- ↑ L'aspiration de l'homme à avoir le melon vient justement de là.
S'il vous a enthousiasmé, votez pour lui sur sa page de vote ! Ou pas.